Stack Based Virtual Machines - 3
This post is part of the Stack Based Virtual Machines series.
In the previous part we have started writing some code for our stack based virtual machine. In this part, we’re going to extend the catalog of instructions that our CPU can support. The code for this article can be found on github.
Arithmetics Link to heading
Our VM can already handle additions, so teaching it to add subtractions, multiplications and (integer) division won’t be very hard. We can start with a few trivial tests:
@Test
public void testSubTwoNumbers() {
CPU cpu = new CPU(PUSH, 1, PUSH, 2, SUB, HALT);
assertProgramRunsToHaltAndInstructionAddressIs(cpu, 6);
assertStackContains(cpu, -1);
}
@Test(expected = InvalidProgramException.class)
public void testSubNeedsTwoItemsOnTheStack() {
CPU cpu = new CPU(SUB, HALT);
cpu.run();
}
// Similar for MUL and DIV
The implementation is quite obvious and we’ll review it in a moment.
But, before, let us discuss a different issue: since our “assembler language” supports only one operation at a time, how can we use it to compute a “complex” expression such as (1 + 2 * 3) / 7? Just as we have seen during our parsing tutorial, we can model it with a tree:
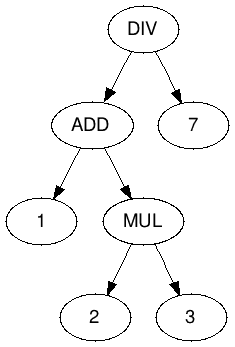
If you’ve ever studied the reverse polish notation - and if you’ve studied stacks you’ve probably seen it - you know we can reorder expressions to avoid parenthesis. In particular we can do a postorder visit on our expression tree and obtain:
1 2 3 MUL ADD 7 DIV
Therefore the following program in our “assembler” would compute the expression:
PUSH 1
PUSH 2
PUSH 3
MUL
ADD
PUSH 7
DIV
If you think a bit about it and simulate the stack, you’ll see that this will compute the correct value. Using this technique, we can compute any arbitrarily complex arithmetic or boolean expression.
Booleans Link to heading
In our virtual machine we’re going to implement booleans in the same way as C does: 0 means false, and any other value will mean true. However, we’ll normalize true to the value 1 as the result of our operations. With this specification, we can add three more instructions: NOT, AND and OR:
@Test
public void testUnaryNotTrue() {
CPU cpu = new CPU(PUSH, 1, NOT, HALT);
assertProgramRunsToHaltAndInstructionAddressIs(cpu, 4);
assertStackContains(cpu, 0);
}
@Test
public void testUnaryNotFalse() {
CPU cpu = new CPU(PUSH, 0, NOT, HALT);
assertProgramRunsToHaltAndInstructionAddressIs(cpu, 4);
assertStackContains(cpu, 1);
}
@Test(expected = InvalidProgramException.class)
public void testNotNeedsOneItemOnTheStack() {
CPU cpu = new CPU(NOT, HALT);
cpu.run();
}
@Test
public void testAndTrueTrue() {
CPU cpu = new CPU(PUSH, 1, PUSH, 1, AND, HALT);
assertProgramRunsToHaltAndInstructionAddressIs(cpu, 6);
assertStackContains(cpu, 1);
}
@Test(expected = InvalidProgramException.class)
public void testAndNeedsTwoItemsOnTheStack() {
CPU cpu = new CPU(AND, HALT);
cpu.run();
}
@Test
public void testOrTrueFalse() {
CPU cpu = new CPU(PUSH, 1, PUSH, 0, OR, HALT);
assertProgramRunsToHaltAndInstructionAddressIs(cpu, 6);
assertStackContains(cpu, 1);
}
@Test(expected = InvalidProgramException.class)
public void testOrNeedsTwoItemsOnTheStack() {
CPU cpu = new CPU(OR, HALT);
cpu.run();
}
Let us now see the (simple) implementation of these instructions:
private void decodeInstruction(int instruction) {
switch (instruction) {
case NOT: {
checkStackHasAtLeastOneItem("NOT");
stack.push(toInt(!toBool(stack.pop())));
break;
}
case ADD:
case SUB:
case MUL:
case DIV:
case AND:
case OR: {
if (stack.size() < 2) {
throw new InvalidProgramException("There should be at least two items on the stack to execute a binary instruction");
}
int n2 = stack.pop();
int n1 = stack.pop();
stack.push(doBinaryOp(instruction, n1, n2));
break;
}
// rest as before
}
}
private void checkStackHasAtLeastOneItem(String instruction) {
if (stack.size() < 1) {
throw new InvalidProgramException("There should be at least one item on the stack to execute an " + instruction + " instruction");
}
}
private Integer doBinaryOp(int instruction, int n1, int n2) {
switch (instruction) {
case ADD:
return n1 + n2;
case SUB:
return n1 - n2;
case MUL:
return n1 * n2;
case DIV:
return n1 / n2;
case AND:
return toInt(toBool(n1) && toBool(n2));
case OR:
return toInt(toBool(n1) || toBool(n2));
default:
throw new AssertionError();
}
}
private boolean toBool(int n) {
return n != 0;
}
private int toInt(boolean b) {
return b ? 1 : 0;
}
The code is perhaps a bit “imperative”, but it’s quite simple.
Stack management instructions Link to heading
To conclude this part, we’re going to add a couple more of instructions to our CPU. The first will be POP, that will simply discard the top item from the stack. The second will be DUP, that will duplicate the top item of the stack.
The tests are as follows:
@Test
public void testPop() {
CPU cpu = new CPU(PUSH, 42, POP, HALT);
assertProgramRunsToHaltAndInstructionAddressIs(cpu, 4);
assertStackIsEmpty(cpu);
}
@Test(expected = InvalidProgramException.class)
public void testPopNeedsAnItemOnTheStack() {
CPU cpu = new CPU(POP);
cpu.step();
}
@Test
public void testDup() {
CPU cpu = new CPU(PUSH, 42, DUP, HALT);
assertProgramRunsToHaltAndInstructionAddressIs(cpu, 4);
assertStackContains(cpu, 42, 42);
}
@Test(expected = InvalidProgramException.class)
public void testDupNeedsAnItemOnTheStack() {
CPU cpu = new CPU(DUP);
cpu.step();
}
The implementation is quite simple:
private void decodeInstruction(int instruction) {
switch (instruction) {
case POP: {
checkStackHasAtLeastOneItem("POP");
stack.pop();
break;
}
case DUP: {
checkStackHasAtLeastOneItem("DUP");
int n = stack.peek();
stack.push(n);
break;
}
// rest as before
}
}
Conclusions Link to heading
We have done enough groundworks; the next part we’re finally going to see how we can implement an “if” statement. And, surprisingly, we’re going to see how close if is to while. :-)
Update: part 4 is online now.