Introduction to Parsing - 9

Published Thursday, Jan 8, 2015 - 1215 words, 6 minutes

Tagged:

c++ ,
parsing

This post is part of the Introduction to parsing series.

In the last part we started adapting our parser to work with an AST, as a step towards handling function definitions. In this part, we’ll continue on that road.

C++11 functions and lambdas Link to heading

Rather than implement four almost equal classes, we are going to implement a basic BinaryOpNode class and then four subclasses. We’ll rewrite AdditionNode as follows:

class BinaryOpNode : public Node {
public:
    using evalFunc = std::function<double(double, double)>;
    using toStringFunc = std::function<std::string(std::string, std::string)>;

    BinaryOpNode(Node &left, Node &right, toStringFunc toString, evalFunc eval)
    : left_(left), right_(right), toString_(toString), eval_(eval) {}
    virtual ~BinaryOpNode() {}

    virtual std::string toString() const override {
        return toString_(left_.toString(), right_.toString());
    }

    virtual double eval(EvaluationContext &context) override {
        return eval_(left_.eval(context), right_.eval(context));
    }

private:
    Node &left_;
    Node &right_;
    toStringFunc toString_;
    evalFunc eval_;
};

class AdditionNode : public BinaryOpNode {
public:
    AdditionNode(Node &left, Node &right)
    : BinaryOpNode(left, right,
        [](std::string s1, std::string s2){return s1 + " + " + s2;},
        [](double v1, double v2){return v1 + v2; }) {}
    virtual ~AdditionNode() {}
};

Before checking the code, let’s discuss std::function. This is a class in the C++ standard library, used to represent a delayed function call: basically it’s an implementation of the Command design pattern. This StackOverflow answer has some good details about why it’s better to use an std::function rather than a “naked” function pointer.

In our case, we’ve used C++11 using syntax to define two types:

using evalFunc = std::function<double(double, double)>;
using toStringFunc = std::function<std::string(std::string, std::string)>;

The syntax means that evalFunc is an object of type std::function, representing a function call that returns a double and takes two doubles. Similarly, toStringFunc is a function call that takes two strings and returns a string.

Our base class BinaryOpNode stores four things:

the left and right nodes, as before
an evalFunc, which is called with the result of the eval call to the left and right node to implement the eval of the binary node
a toStringFunc, analogous to the previous one for toString.

We can now focus on the AdditionNode class: as you can see, it simply delegates everything to the base class. The eval_ and toString_ members in the base class are initialized by using two C++11 lambdas. Let’s focus on the initializer for eval_; the other is very similar. What we wrote is:

    [](double v1, double v2){return v1 + v2;}

We have a pair of square brackets, which are used to define the captures, which are basically used to implement what in other languages would be called “a closure”. In our case, we don’t have to use any variable in the parent scope, so we use an empty pair of brackets.

Next are a pair of parenthesis, defining the parameters of the lambda function. In this case, we have two doubles.

Last is a standard block, containing the code of the lambda function.

This is how our function would look in Python for comparison:

    lambda v1, v2: v1 + v2

and in Javascript:

    function(v1, v2) {return v1 + v2;}

Finally, after this syntax tour, we should be able to understand all the code. For reference, the other three nodes classes are about as you’d expect:

class SubtractionNode : public BinaryOpNode {
public:
    SubtractionNode(Node &left, Node &right)
            : BinaryOpNode(left, right,
            [](std::string s1, std::string s2){return s1 + " - " + s2;},
            [](double v1, double v2){return v1 - v2; }) {}
    virtual ~SubtractionNode() {}
};

class MultiplicationNode : public BinaryOpNode {
public:
    MultiplicationNode(Node &left, Node &right)
            : BinaryOpNode(left, right,
            [](std::string s1, std::string s2){return s1 + " * " + s2;},
            [](double v1, double v2){return v1 * v2; }) {}
    virtual ~MultiplicationNode() {}
};

class DivisionNode : public BinaryOpNode {
public:
    DivisionNode(Node &left, Node &right)
            : BinaryOpNode(left, right,
            [](std::string s1, std::string s2){return s1 + " / " + s2;},
            [](double v1, double v2){return v1 / v2; }) {}
    virtual ~DivisionNode() {}
};

Noticed the bug? Link to heading

As you might have noticed, our code is bugged. If we built a tree with this structure:

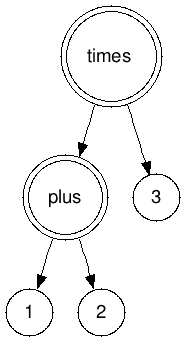
and called toString on the root (times) node, we would get 1 + 2 * 3, which is a different expression! Our tree structure makes parenthesis implicit, but that doesn’t mean that they can be ignored in the toString method. :-)

So, let’s fix our code. There are multiple ways to do it; what we’ll do is to add a boolean parameter to toString, which represents whether the method should be interpreted as “being called as the root node” or “being called as a sub node”. This allows us to adapt the tests as follows:

    CASE("NumberNode") {
        NumberNode node(0.5);
        EXPECT("0.5" == node.toString(true));
        EXPECT("0.5" == node.toString(false));
        EXPECT(approx(0.5) == evalNode(node));
    },

    CASE("AdditionNode") {
        NumberNode n1(1), n2(2);
        AdditionNode node(n1, n2);
        EXPECT("1 + 2" == node.toString(true));
        EXPECT("(1 + 2)" == node.toString(false));
        EXPECT(approx(3) == evalNode(node));
    },
    CASE("SubtractionNode") {
        NumberNode n1(1), n2(2);
        SubtractionNode node(n1, n2);
        EXPECT("1 - 2" == node.toString(true));
        EXPECT("(1 - 2)" == node.toString(false));
        EXPECT(approx(-1) == evalNode(node));
    },
    CASE("MultiplicationNode") {
        NumberNode n2(2), n3(3);
        MultiplicationNode node(n2, n3);
        EXPECT("2 * 3" == node.toString(true));
        EXPECT("(2 * 3)" == node.toString(false));
        EXPECT(approx(6) == evalNode(node));
    },
    CASE("DivisionNode") {
        NumberNode n1(1), n2(2);
        DivisionNode node(n1, n2);
        EXPECT("1 / 2" == node.toString(true));
        EXPECT("(1 / 2)" == node.toString(false));
        EXPECT(approx(0.5) == evalNode(node));
    },

    CASE("Recursive Nodes") {
        NumberNode n1(1), n2(2), n3(3);
        MultiplicationNode n2times3(n2, n3);
        AdditionNode node(n2times3, n1);
        EXPECT("(2 * 3) + 1" == node.toString(true));
        EXPECT(approx(7) == evalNode(node));
    },
    CASE("Recursive Nodes 2") {
        NumberNode n1(1), n2(2), n3(3), n4(4), n7(7);
        AdditionNode n1plus3(n1, n3);
        DivisionNode n4dividedBy2(n4, n2);
        SubtractionNode n7minusn4dividedBy2(n7, n4dividedBy2);
        DivisionNode node(n1plus3, n7minusn4dividedBy2);
        EXPECT("(1 + 3) / (7 - (4 / 2))" == node.toString(true));
        EXPECT(approx(0.8) == evalNode(node));
    }

(Note: as I look at the code now, I’ve noticed that I should really have created an enum rather than used a raw boolean parameter. I’m going to change this in a following commit.)

The changes required to pass the test are quite simple:

class Node {
	// The only change is:
    virtual std::string toString(bool isTopLevel) const = 0;
};

class NumberNode : public Node {
	// No change except in the function signature
};

class BinaryOpNode : public Node {
	// Only toString changes as follows:
    virtual std::string toString(bool isTopLevel) const override {
        std::string s = toString_(left_.toString(false), right_.toString(false));
        return isTopLevel ? s : "(" + s + ")";
    }
};

// No changes in the various subclasses of BinaryOpNode

Conclusions Link to heading

This part was a bit more about some “new” C++11 features than about parsing; I hope you won’t mind. In the next parts we are going to complete our catalog of nodes, by adding a node that accesses a variable’s value and another to call a function. Afterwards, we’ll go back to our parser and start adapting it to use our nodes.

More nodes type Link to heading

C++11 functions and lambdas Link to heading

Noticed the bug? Link to heading

Conclusions Link to heading