Introduction to Parsing - 8

In the last part we made our parser work with variables. In this part, we’ll take a step back and start setting up the infrastructure for handling function definitions.

Immediate evaluation vs AST Link to heading

Our parser is currently working in an “immediate evaluation” mode: as soon as a token is found, it is evaluated. While this has worked well for us so far, it will cause problem when we’ll move towards letting the user define functions: we need to delay evaluation of the functions until needed. A “cheap” solution would be to store function definitions as the sequence of tokens, but that would not really help us towards calculating derivatives, which is our goal. So, a different approach is required.

Let’s take a step back and think about what we do when handling an expression like 1 + 2. Our parsers starts evaluating the expression, meaning it evaluates a term, meaning it evaluates a factor, meaning it evaluates the number 1. Then it notices (in the expression parsing) a + token, and thus repeats the term parsing. Finally, having evaluated the left-side and right-side of the + operator, it sums them and returns the result.

This can be modeled by this simple tree:

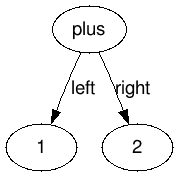
If we had instead something like 1 + 2 * 3 we can imagine it to be modeled by this tree:

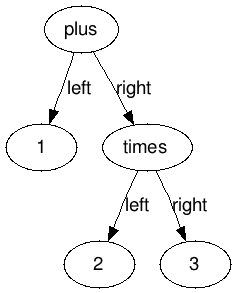
In general, we can imagine to model all the expressions our parser can understand with trees. This kind of trees are usually called Abstract Syntax Trees or AST for short. Quoting from wikipedia:

In computer science, an abstract syntax tree (AST), or just syntax tree, is a tree representation of the abstract syntactic structure of source code written in a programming language. Each node of the tree denotes a construct occurring in the source code. The syntax is “abstract” in not representing every detail appearing in the real syntax. For instance, grouping parentheses are implicit in the tree structure, and a syntactic construct like an if-condition-then expression may be denoted by means of a single node with three branches.

Towards an expression tree Link to heading

In this and the next posts we are going to slowly transform our parser, so that instead of immediately evaluating expressions, it is going to build a tree representing the input. After this changes, we’ll be well on the way to handle both function definitions and derivatives: an user-defined function will be (roughly) mapped to the syntax tree built from its definition, and we’ll operate on the tree to calculate the function’s derivative.

Let’s start: the first commit is here. We are going to define an abstract base class named Node:

class Node
{
public:
    virtual ~Node() {}

    virtual std::string toString() const = 0;
    virtual double eval(EvaluationContext &context) = 0;
};

Saying that a method is virtual and = 0 is C++’s syntax to mark it as abstract, meaning that all the subclasses will have to implement it. In this case, we have two methods that all the subclasses must implement:

• toString, to get a representation of the node as string, suitable for displaying to the user
• eval, to get the node’s value.

The new EvaluationContext is this:

// A doubleToDoubleFunction is a pointer to a function taking a double and returning a double
using doubleToDoubleFunction = double(*)(double);
using functionMap = std::map<std::string, doubleToDoubleFunction>;
using variablesMap = std::map<std::string, double>;

struct EvaluationContext {
    functionMap &functions;
    variablesMap &variables;

    EvaluationContext(functionMap &funcs, variablesMap &vars)
        : functions(funcs), variables(vars) {
    }
};

It will be needed when we’ll implement nodes representing a variable access or a function call.

Let’s go back to the basics and see our first node type, NumberNode. This is a node representing a factor of type number in our grammar. The class is pretty much as you can imagine it:

class NumberNode : public Node {
public:
    NumberNode(double n) : n_(n) {}
    virtual ~NumberNode() {}

    virtual std::string toString() const override {
        std::ostringstream oss;
        oss << n_;
        return oss.str();
    }

    virtual double eval(EvaluationContext &context) override {
        return n_;
    }

private:
    double n_;
};

Other than for the C++- syntax: its constructor takes a number which is saved in the private member n_. When eval is called, n_ is returned. Finally, we use std::ostringstream to print the number as a string. We could also have used the new C++11 std::to_string function, but I found that its output had a lot of decimal digits without a simple way to specify how many, so I’ve relied on the older ostringstream.

We have used the new C++11 keyword override to explicitely mark the virtual methods that we are overriding. Just as @Override in Java, using this keyword tells the compiler to throw an error in case we are not overriding a base function for some reasons, which can be quite helpful.

Before moving on, let’s see the trivial unit test:

// Helper function that creates an "empty" EvaluationContext
double evalNode(Node &node) {
    functionMap functions;
    variablesMap variables;
    EvaluationContext ec(functions, variables);

    return node.eval(ec);
}

const lest::test testNode[] = {
    CASE("NumberNode") {
        NumberNode node(0.5);
        EXPECT("0.5" == node.toString());
        EXPECT(approx(0.5) == evalNode(node));
    }
};

Additions Link to heading

Let’s move on to something more interesting, like additions. Thinking back to our earlier 1 + 2 example, the structure of the AdditionNode class should be quite obvious:

class AdditionNode : public Node {
public:
    AdditionNode(Node &left, Node &right) : left_(left), right_(right) {}
    virtual ~AdditionNode() {}

    virtual std::string toString() const override {
        return left_.toString() + " + " + right_.toString();
    }

    virtual double eval(EvaluationContext &context) override {
        return left_.eval(context) + right_.eval(context);
    }

private:
    Node &left_;
    Node &right_;
};

Notice that we explicitely made the decision to use a binary tree structure: each addition node will have two children. This means that an expression such as 1 + 2 + 3 must be expressed like this:

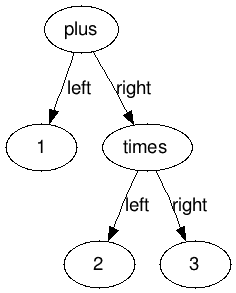
or like this:

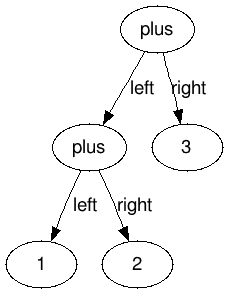
The other possibility would be for an AdditionNode to have a list of children. However, binary tree tend to be easier to reason about and to implement, and (in this case) just as expressive, so we have decided to follow that road.

The tests are, again, pretty much as expected:

    CASE("AdditionNode") {
        NumberNode n1(1), n2(2);
        AdditionNode node(n1, n2);
        EXPECT("1 + 2" == node.toString());
        EXPECT(approx(3) == evalNode(node));
    },
    CASE("Recursive AdditionNode") {
        NumberNode n1(1), n2(2), n3(3);
        AdditionNode n1plus2(n1, n2);
        AdditionNode node(n1plus2, n3);
        EXPECT("1 + 2 + 3" == node.toString());
        EXPECT(approx(6) == evalNode(node));
    }

Conclusions Link to heading

In this (slightly shorter than usual) post we have started the groundwork for allowing the user to define functions in our language. The next time we’ll implement the other three operations, learn a bit about C++11 lambdas and handle parenthesis.