Introduction to Parsing - 1

In this posts series, we’re going to dive a bit into parsing. The idea is to eventually build a very simple language that can calculate mathematical derivative. That is, we want to be able to write things like:

> f(x) := x^3 + 2 * x - sin(x)
> f'
3 * x ^ 2 + 2 - cos(x)

It’s going to take a while to get there, but don’t worry, it will be fun and hopefully you’ll find it interesting.

Show me the code Link to heading

You can download the project or check it out online from its GitHub home.

The code is written in C++, mostly to give myself an excuse to play with C++11 and CMake. I’ll try to keep the C++-abuse to a minimum, to help make the code readable for those unfamiliar with it.

Let’s take a look at how the code is organized. There are three top-level directories, libs which only contains lest, a neat and simple unit-testing framework for C++. I like it very much because it’s all contained in one .h file, which makes it very easy to include in any project.

The folder sources contains the actual code, where tests contains the unit tests. For the moment we have no main in our program, but only some unit tests.

Lexers Link to heading

We are going to start with the lexer. Lexers, as wikipedia teaches us, are programs or functions that perform lexical analisys, where

lexical analysis is the process of converting a sequence of characters into a sequence of tokens, i.e. meaningful character strings.

So, in short, we are going to write a lexer to split the input into pieces called tokens. Next we’ll write the parser, that will interpret the tokens sequence and give it a meaning. Let’s start to take a look at the code. For the moment we only want to hanlde very simple inputs, such as 1, 1+23 or (1+23)*4. We aren’t goint to be able to handle spaces in this very first version of our lexer, but we will be adding that shortly.

Tokens and token types Link to heading

In our very simple language, we’re going for the moment to have only two types of tokens: numbers and operators. Furthermore, we’ll only handle integer numbers. So we can start in token.h with

enum TokenType
{
    OPERATOR,
    NUMBER
};

and with a very simple (immutable) Token class:

class Token
{
public:
    Token(TokenType tokenType, std::string content)
        : tokenType_(tokenType), content_(content) {}

    inline TokenType getTokenType() const {
        return tokenType_;
    }

    inline std::string getContent() const {
        return content_;
    }

    inline bool operator ==(const Token& other) const {
        return tokenType_ == other.tokenType_
            && content_ == other.content_;
    }

private:
    TokenType tokenType_;
    std::string content_;
};

Tests Link to heading

Now we can take a look at the unit tests. We can start by writing some very simple cases to handle in testLexer.cpp:

const lest::test specification[] = {
    CASE("parsing '1'") {
        std::istringstream input{"1"};
        Lexer lexer(input);
        EXPECT(lexer.hasNextToken());

        EXPECT(lexer.nextToken() == Token(NUMBER, "1"));

        EXPECT_NOT(lexer.hasNextToken());
    },

    CASE("parsing '1+23'") {
        std::istringstream input{"1+23"};
        Lexer lexer(input);
        EXPECT(lexer.hasNextToken());

        EXPECT(lexer.nextToken() == Token(NUMBER, "1"));
        EXPECT(lexer.hasNextToken());

        EXPECT(lexer.nextToken() == Token(OPERATOR, "+"));
        EXPECT(lexer.hasNextToken());

        EXPECT(lexer.nextToken() == Token(NUMBER, "23"));
        EXPECT_NOT(lexer.hasNextToken());
    },

    CASE("parsing '(1+23)*4'") {
        std::istringstream input{"(1+23)*4"};
        Lexer lexer(input);
        EXPECT(lexer.hasNextToken());

        EXPECT(lexer.nextToken() == Token(OPERATOR, "("));
        EXPECT(lexer.nextToken() == Token(NUMBER, "1"));
        EXPECT(lexer.nextToken() == Token(OPERATOR, "+"));
        EXPECT(lexer.nextToken() == Token(NUMBER, "23"));
        EXPECT(lexer.nextToken() == Token(OPERATOR, ")"));
        EXPECT(lexer.nextToken() == Token(OPERATOR, "*"));
        EXPECT(lexer.nextToken() == Token(NUMBER, "4"));

        EXPECT_NOT(lexer.hasNextToken());
    }
};

Basically we are writing simple assertions to extract the tokens in order, using the Lexer class that we’ll see in a moment and its function nextToken. We are also checking that the function hasNextToken returns true when we have something to take, and false otherwise.

The Lexer Link to heading

As you might have guessed by the tests, our Lexer class’s constructor takes an std::istream & as its only argument:

class Lexer
{
public:
    explicit Lexer(std::istream& istream);
    Token nextToken();
    bool hasNextToken() const;

private:
    std::istream& istream_;
    char next_;
    bool atEof_;

    void advance();
    Token parseNumber();
    Token parseOperator();
};

To implement easily the hasNextToken, we’re going to use a lookahead character. Basically, we’re going to store the next_ character in the stream and use it to decide whether we have something to parse or not. We’re also going to keep track of whether the last get call to the istream ended up in eof. This is going to be an invariant of our class, so we’re going to start this in the constructor and keep it true in any method. Furthermore, the only method that is going to directly touch the istream is going to be advance.

Let’s see the constructor now:

Lexer::Lexer(std::istream& istream)
    : istream_(istream), atEof_(false)
{
    advance();
}

To keep the invariant, we’re going to start off by immediately call advance, to initialize the next_ and atEof_ variables.

We can move on to the very simple methods advance and hasNextToken now:

void Lexer::advance()
{
    next_ = static_cast<char>(istream_.get());
    atEof_ = istream_.eof();
}

bool Lexer::hasNextToken() const
{
    return !atEof_;
}

Numbers and operators Link to heading

It is now time to see the juice of our lexer: the method nextToken. This method will use the lookahead to detect whether we’ve encountered a number or not. In this second case, we’ll treat anything as a single-character operator, meaning that abc would be parsed as the sequence of operators a, b, c, which probably doesn’t make much sense… Nevertheless, here’s nextToken in all its glory:

Token Lexer::nextToken()
{
    if (atEof_) {
        throw std::runtime_error("EOF");
    }

    if (std::isdigit(next_)) {
        return parseNumber();
    } else {
        return parseOperator();
    }
}

Let’s focus first on parseOperator. Remember that we have to keep the invariant valid, so we’re going to have to call advance before returning to ensure that the lookahead points to the first unparsed character:

Token Lexer::parseOperator()
{
    Token result = Token{OPERATOR, std::string{next_}};
    advance();
    return result;
}

parseNumber is slightly more complex. It, too, has to keep the invariant valid, but furthermore it doesn’t know where to stop: it has to go on until it finds digits. So, here’s the code:

Token Lexer::parseNumber()
{
    std::string num;
    while (!atEof_ && isdigit(next_)) {
        num += next_;
        advance();
    }

    return Token{NUMBER, num};
}

Notice how we add next_ to num before calling advance().

Somebody said FSM? Link to heading

If you’ve ever met finite-state machines, you might have recognized one in our lexer. Basically we can model our lexer with this:

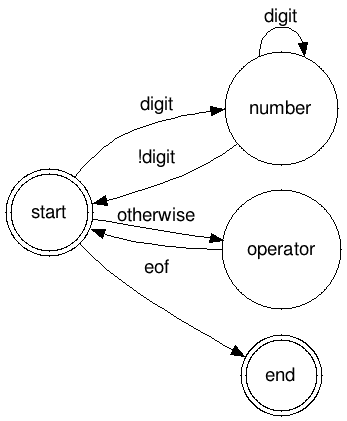
This (bad looking) graph means that our lexer starts in the start status. If it finds a digit, it moves to the number status. Afterwards, it keeps staying in the number status while it finds digit, and then returns to the start status. If it encounters any other character, it goes to the operator status, from which it immediately returns. Finally, if there are no more characters in the input (eof), it goes to the end status.

Next time Link to heading

Next time we’re going to extend our simple lexer so that it can handle spaces and restrict the set of operators allowed.

Credits Link to heading

The FSM figure was created using Erdos, an online Graphviz engine. The source code for the image can be found at this gist.